Garry's Mod Wiki

Home / math.CHSpline

math.CHSpline

  Vector math.CHSpline( number frac, Vector point0, Vector tan0, Vector point1, Vector tan1 )
Search Github

Description

Cubic Hermite spline algorithm.

Arguments

1 number frac
From 0 to 1, where alongside the spline the point will be.
2 Vector point0
First point for the spline.
3 Vector tan0
Tangent for the first point for the spline.
4 Vector point1
Second point for the spline.
5 Vector tan1
Tangent for the second point for the spline.

Returns

1 Vector
Point on the cubic Hermite spline, at given fraction.

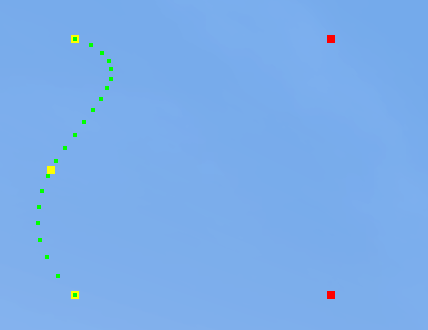
Example

local points = { Vector( 128, 128 ), -- point 1 Vector( 384, 128 ), -- tangent pos 1 Vector( 128, 384 ), -- point 2 Vector( 384, 384 ) -- tangent pos 2 } hook.Add( "HUDPaint", "math.BezierLerp", function() local frac = RealTime() % 1 local point = math.CHSpline( frac, unpack( points ) ) surface.SetDrawColor( 255, 255, 0 ) surface.DrawRect( point.x - 4, point.y - 4, 8, 8 ) surface.DrawRect( points[1].x - 4, points[1].y - 4, 8, 8 ) surface.DrawRect( points[3].x - 4, points[3].y - 4, 8, 8 ) surface.SetDrawColor( 255, 0, 0 ) surface.DrawRect( points[2].x - 4, points[2].y - 4, 8, 8 ) surface.DrawRect( points[4].x - 4, points[4].y - 4, 8, 8 ) -- Draw the spline for i=0,20 do local point = math.CHSpline( i / 20, unpack( points ) ) surface.SetDrawColor( 0, 255, 0 ) surface.DrawRect( point.x - 2, point.y - 2, 4, 4 ) end end )
Output:
image.png

Account Management

Special Pages

Wiki List