Mesh Library References

These pages seek to provide helpful insight into the usage of the Mesh library and its functions.

The pages in this series are:

• Primitive Types

Terms and Definitions

What is a Primitive?

Definitionally, a Primitive is the simple shapes that any model (or "Mesh") is built from.
Practically, a Primitive is a grouping of one or more vertices that the rendering system interprets together in order to draw a simple shape onto the currently active Render Target.

As an example, the most common Primitive types are triangles (3 vertices), and quads (4 vertices).

Vertex Winding

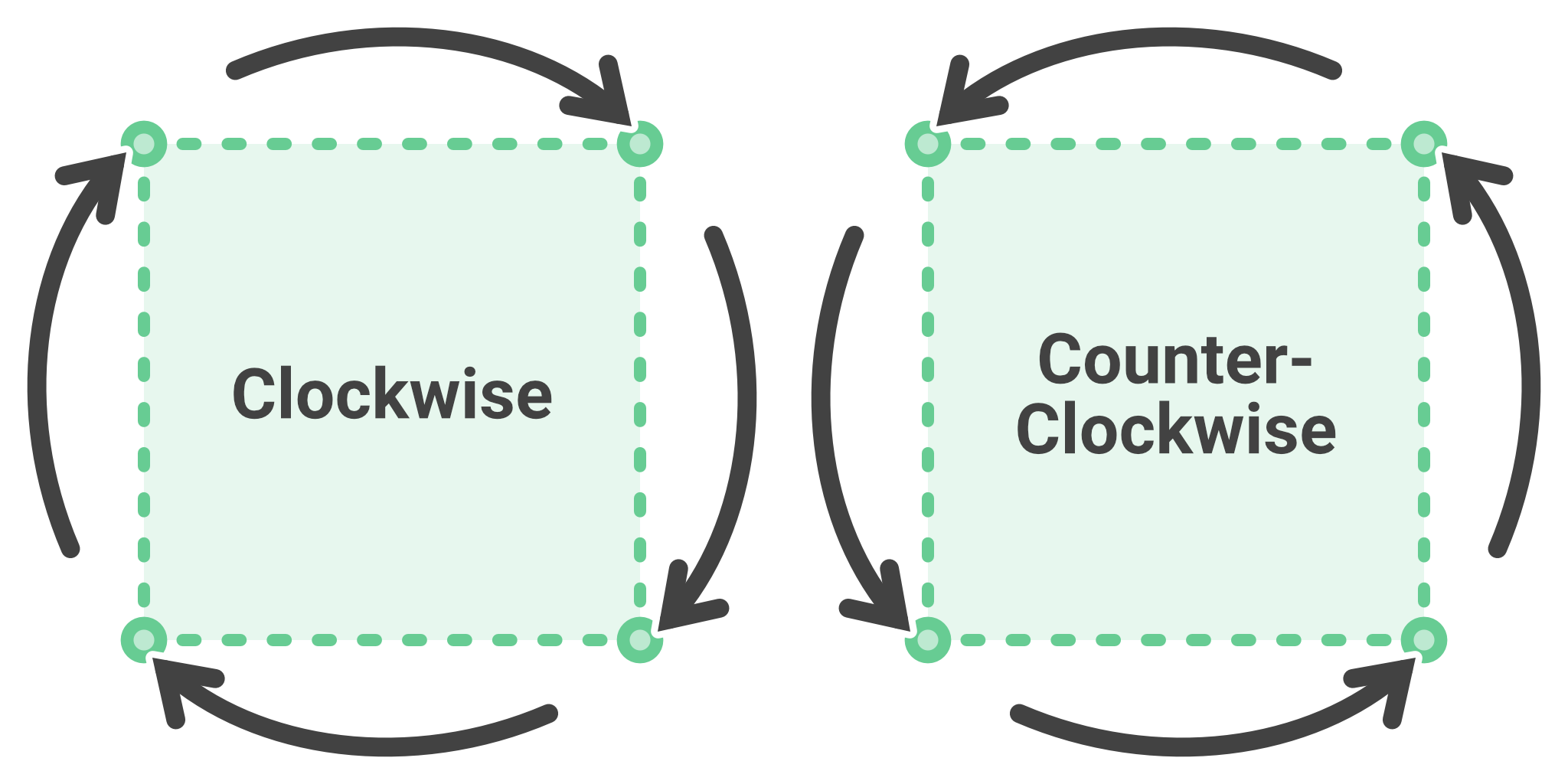
When defining a Primitive, the order of its vertices is very important for ensuring it draws as expected. The rendering system does not perform any meaningful validation of the Primitive's information and instead simply draws whatever data it is provided. Because of this, it is important to provide vertices in the order that the rendering system is expecting.

There are two ways of ordering verticies (Called "Windings"): Clockwise and Counter-Clockwise (or Anti-Clockwise, if preferred.)

Fun fact: They're called "Windings" because putting lines between vertices is conceptually similar to winding a rope or wire around a spool!

Culling

To save on unnecessary draw operations, the rendering system only draws Primitives (or "faces") that are facing generally towards the camera.
The way that the rendering system determines which faces to draw and which faces not to draw is based on the vertex winding of the face in question.

If a face is wound counter-clockwise relative to the camera, it is assumed to be a "front" face (which is drawn), and if it is instead wound clockwise relative to the camera, it is considered a "back" face (Which is not drawn.)

This type of culling is often called "back face culling" and it is the major reason why vertex order is important when creating Meshes.

In rare cases, it may be necessary to temporarily override the normal winding order by using render.CullMode immediately before and after the rendering operation.

Types of Primitive

Points

The Points Primitive type (Also called a "Point List") interprets each of the Mesh's vertices as a standalone point in space.
When rendered, each of these points appears as a single pixel.

Lines

The Lines Primitive type (Also called a "Line List") interprets the Mesh's vertices in pairs of 2 where each pair of vertices represents the start and end points for a line.

Because each line requires a start and end point, the total number of vertices must be evenly divisible by 2.

Triangles

As the names suggests, Triangle Primitives (Also called a "Triangle List") groups every 3 of the Mesh's vertices together and draws a textured triangle between them.

Because each triangle requires exactly 3 points, the Mesh's total vertex count must be a multiple of 3.

The direction the resulting triangle faces is determined by the current render.CullMode as well as the order that the vertices were added to the Mesh.

Triangle Strips

Triangle Strip Primitives are a convenience feature to make it easier to create sequences of triangles that each share an edge with the previous triangle in the sequence.

The first triangle in the sequence is created using the first 3 vertices added to the Mesh. All subsequent triangles are created using just 1 additional vertex in addition to the final 2 vertices of the previous triangle in the sequence.

This method uses fewer total vertices than would be required to create them using the Triangles Primitive type, which makes it more performant than creating those same triangles individually.

Example

Line Strips

The Line Strip Primitive type defines a sequence of lines that are each connected to the previous line in the sequence.

The first line in the sequence is defined by the first 2 vertices in the Mesh and each additional vertex defines a new segment of the line starting at the previous line's end point.

Line Loops

A Mesh using the Line Loop Primitive behaves identically to the Line Strip Primitive with the notable addition of a final line connecting the first and last vertices in the sequence.

Polygons

Polygon Primitives

Quads

Quad Primitives